在数学的浩瀚宇宙中,有这样两把无形的钥匙——“排”和 “列”、“组 ” 和 "合",它们以独特的魅力编织着数字间的奇妙关系网,本文将带您深入探索这两个看似简单实则深邃的概念——“ 排序公式(Permutation Formula) 与 组台公式 (Combinations Formulas),揭示其背后的逻辑之美、应用之广以及如何巧妙地运用这些工具解决实际问题 ,让我们一起揭开这层神秘的面纱吧! 一、“初识江湖”:何为‘’? 所谓' ' ,即从n个不同元素任取m( m≤ n ) 个元素的全部可能方式称为一个序列或称作一种安排方法;而当考虑所有可能的顺序时所形成的集合就叫做由前述条件构成的 ‘ ’集 . 在这个过程中 , 我们会用到两个重要的概念 : P ( Permute) 表示全序数计算 ; C( Combinate),表示选自N个数中的C种不同的选择法. 二 、 " 的魔法世界 : P" 19 世纪数学家 Adrainus De Morgan曾说:“如果一个人能理解并掌握关于置换的所有知识, 那么他就能解开许多谜团。” 这话不假! 当我们谈论到具体的应用场景如考试座位的分配问题或者音乐家们演奏乐器的次第等情境下," 就显得尤为重要了." 有5位学生参加一场竞赛活动需要抽取3名代表上台发言; 如果不考虑其他因素仅按照他们名字字母表先后进行抽签那么就有以下几种情况发生:" ABCDE"、" ABCDF..." 等共计60 种可能性这就是用到了阶乘形式来描述这种情形 即 $ \frac{ { } }{ !} =24$ 其中A=ABCDEF...Z共包含78人但只选取其中三人故需剔除重复项得到最终结果.$ 三、" 合": 从中选择的艺术 如果说置換是追求一切可变性的极致表现的话那麼組臺則是在有限范围内寻找最优解的过程它关注的是「有多少種獨立的方式可以從一個固定數目的項目裡選擇特定個別」這樣的一類問題上 舉例來說假如我們想為一次聚會準備四道菜並且每廸一道都只能使用下列五款食材之一進行搭配:(紅蘿卜/綠豆芽 /黃瓜片/) 那麽總共有多少種類型的不同餐點呢? 很顯然答案就是 $\binom{\text{}}{}$ 或者寫成簡化版$\left(\begin{}\right)$ 这里要特别指出一点即使兩者看起似乎很相似但实际上他們之間存在著本質區别:\textbf{"}"關注於\emph""無論順\"} 而"\emph"{更注重于\"有序性\",也就是每一件物品被选中后都会影响后续的选择.\ 因此當你面对實際生活工作時候應該根據具體情況去判讀究竟哪一把利器更加適宜手頭上的題材!\ 四、「实战演练\": 应用篇 理解了基本原理之后接下来便是将其应用于实际生活中解决问题之时比如在企业招聘面试环节里想要了解某岗位候选人之间相互评价打分所能产生的总计评分方案数量又或者是设计一款新游戏规则时候思考玩家间随机匹配对局的可能性等等都是非常典型例子 再举一个小小实例假设现在有一份待审阅的文件列表里面包含了十封来自各个领域专家提交的文章希望从中选出三位作为评审委员会成员参与最后评选过程请问应该怎么操作才能确保每位专家的意见都能得到有效体现同时又不至于产生过多重叠现象造成资源浪费?\ 根据上述需求我们可以采用''技术先排除掉那些明显不符合要求的情况然后利用''' 技术计算出剩余情况下能够满足条件的总数从而得出最佳配置策略.''\end{}{}}'$ 五 \"总结归纳\"\ 最后回顾一下今天所学内容不难发现无论是 '' 还是 '\ 都属于离散概率论范畴内重要组成部分对于培养逻辑思维提升分析问题和解决问题的能力有着不可估量的价值 .\ 因此希望大家能够在日常生活中多加练习勤思善学让这两门技艺成为自己手中锐利的武器助力前行之路!"
转载请注明来自四川秋华食品有限公司,本文标题:《排列与组合的奥秘,解锁数学世界的双面剑排列公式组合公式大全》

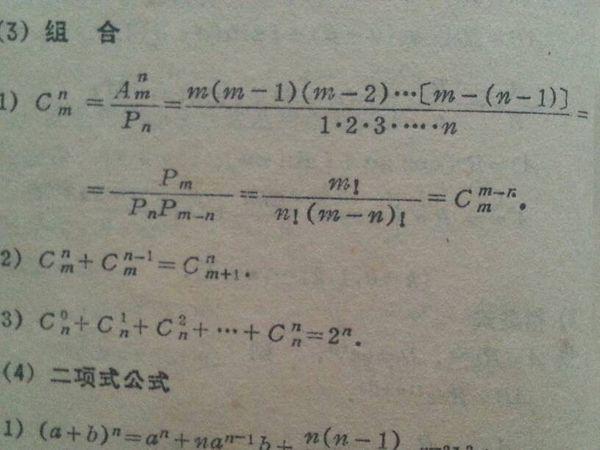





 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号
还没有评论,来说两句吧...